Zero configuration
When you upload a file of geographic data to Felt, we convert it from its original format—perhaps GeoJSON, Shapefile, KML, GeoPackage, CSV, Excel, or GPX—into a set of vector map tiles at a variety of zoom levels, ensuring that any location in the world can be displayed quickly and efficiently at any scale. Unlike some other mapping services, we don’t require you to tell us anything else about the data you are uploading or how you want it to be processed: these questions are often difficult to answer, and we want your uploading experience to be as smooth and straightforward as it can be.
One key question that we must be able to answer for every uploaded file is, what is the appropriate scale at which to display this data? Sometimes it might be obvious from the geographic scope of the contents: a file of the borders of the countries of the world is probably meant to be displayed at a global scale; a file of the trees in one city park is probably meant to be displayed at a scale where the individual trees can be distinguished. But sometimes a broad geographic scope can be misleading or ambiguous: is a file of all the roads in the US meant to be viewed as a map of the country, or as a collection of maps of towns and cities and neighborhoods?
We take the broad view of these possibilities, and therefore we actually must answer two questions: what is the smallest scale, the highest zoom level, at which it makes sense to display this data, and how can we best generalize it to maintain efficiency and visual integrity as you zoom out to view larger areas of it at once?
Generalization and polygon dust
Some types of geographic objects have an inherent physical scale. These are typically mapped as polygons denoting their physical extent on the ground. Examples include building footprints, the land parcels that the buildings sit upon, and the cities, countries, and continents that contain them. All of these experience a kind of natural generalization as you zoom out to look at them from a distance, because small shapes eventually become so small that you can no longer see them, and large shapes become less detailed because their outlines occupy fewer pixels on the screen.
Something similar happens with linear features like roads. The road’s width is not recorded as part of its shape in the data file, only its length, but as you zoom out, short segments of roads nevertheless become so short that they can no longer be seen. They drop out visually, and cease to be represented in the map tiles, while the longer road segments that still are visible are shown more coarsely than before, because no finer detail can be shown on the screen.
But if you are looking down at the ground from an airplane at the same area you see on your laptop screen, even though you may not be able to make out individual buildings because of the great distance from your altitude, you can nevertheless see where there are buildings. They are still visible in the aggregate even though their individual shapes are lost.
Tippecanoe, the software that we use to convert geographic data to map tiles at Felt, tries to mimic this effect through what I call “polygon dust.” At any given scale, polygons that have a size larger than a pixel on the screen are treated as individual distinct objects as you would expect. But polygons that are smaller than this threshold are treated statistically, as the probability of a feature appearing in that location. Even if each of the buildings in a town is too small individually to be displayed, the cluster of buildings accumulates enough probability in the area that a few features, exaggeratedly large compared to their actual size, but only just large enough to be seen on the screen, are carried forward into the map tiles to represent the presence of the town.
.jpg)
Dot-dropping
The other type of data that appears in geographic uploads has no inherent physical magnitude, even in a single dimension. These are point features, often representing street addresses, place names, businesses, photo locations, street intersections, trees, signs, or other points of interest. Because these features are represented as points, which have no size, they never naturally shrink away to nothing as you view larger and larger areas. Instead, we must intentionally drop some point features at lower zoom levels to prevent the map from becoming overwhelmingly visually dense and the data behind it too large to render efficiently.
Tippecanoe is unusual among mapping software in treating this dot-dropping as part of the automatic course of affairs for any point data being made into tiles. Other programs for making map tiles generally either try to preserve every point in every zoom level, until there are so many that it is no longer possible, or rely on the data creator to designate certain features—capitals and other particularly well-known cities, for example—as having higher priority, to be preserved when you zoom out at the expense of other, less significant point features. Tippecanoe instead tries to trick you visually: to thin out the set of points as you zoom out, but slowly enough that you won’t notice any given point vanishing until it is already buried in a cluster of other points and has lost its independent visual identity.
Tippecanoe’s default behavior, if you don’t specify otherwise, is to retain 40% of the point features at the zoom level below the maximum; 40% of those at the next lower zoom level; 40% of those at the next lower zoom level; and so on until it runs out of features or reaches zoom level 0, the zoom level that shows the entire world in one tile. (At Felt we now do specify otherwise, as will be described below.)
The distances between features
I have been talking about generalizing and dropping features as you zoom out, without saying what scale it is that you are zooming out from.
There is a fundamental tension in the choice of the maximum zoom level at which we will generate map tiles for a given upload: we want it to be as high as possible, because higher zoom levels have higher spatial precision than lower zoom levels, and we want to faithfully represent all of the locations in the uploaded data; but we also want it to be as low as possible, because each increase to the maximum zoom level roughly doubles the time it takes to create map tiles, and we want to give users access to their data as quickly as possible after they upload it.
What compromise can we make, then? The principle I have tried to establish is that the appropriate maximum zoom level is the lowest zoom level where you can tell the features apart from each other. Now let’s pick that apart.
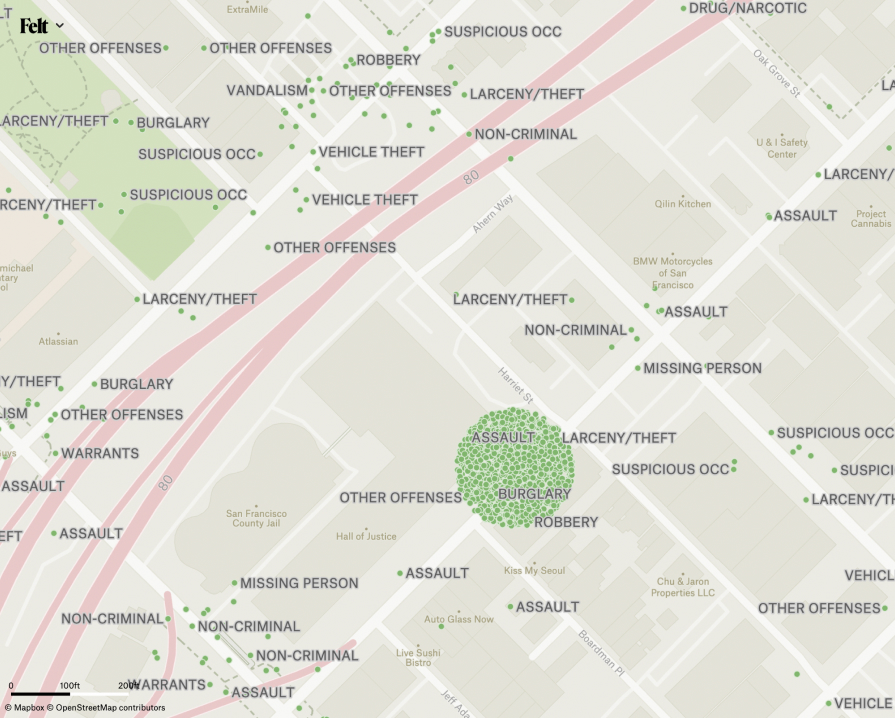
To choose the zoom level at which it will be possible to tell all the features apart from each other, we might find the closest pair of points in the input data and then calculate the distance between them. This smallest distance is often impractical, though. In many cases, the two closest points are actually directly on top of each other, for example in the case of San Francisco’s crime report data, where all the crimes whose location is unknown are geocoded with the point location of police headquarters. Even when there are no exact duplicates, the distance between the closest pair of points is often a statistical outlier rather than representative of the distances between features in the larger data set.



.png)












.jpg)




